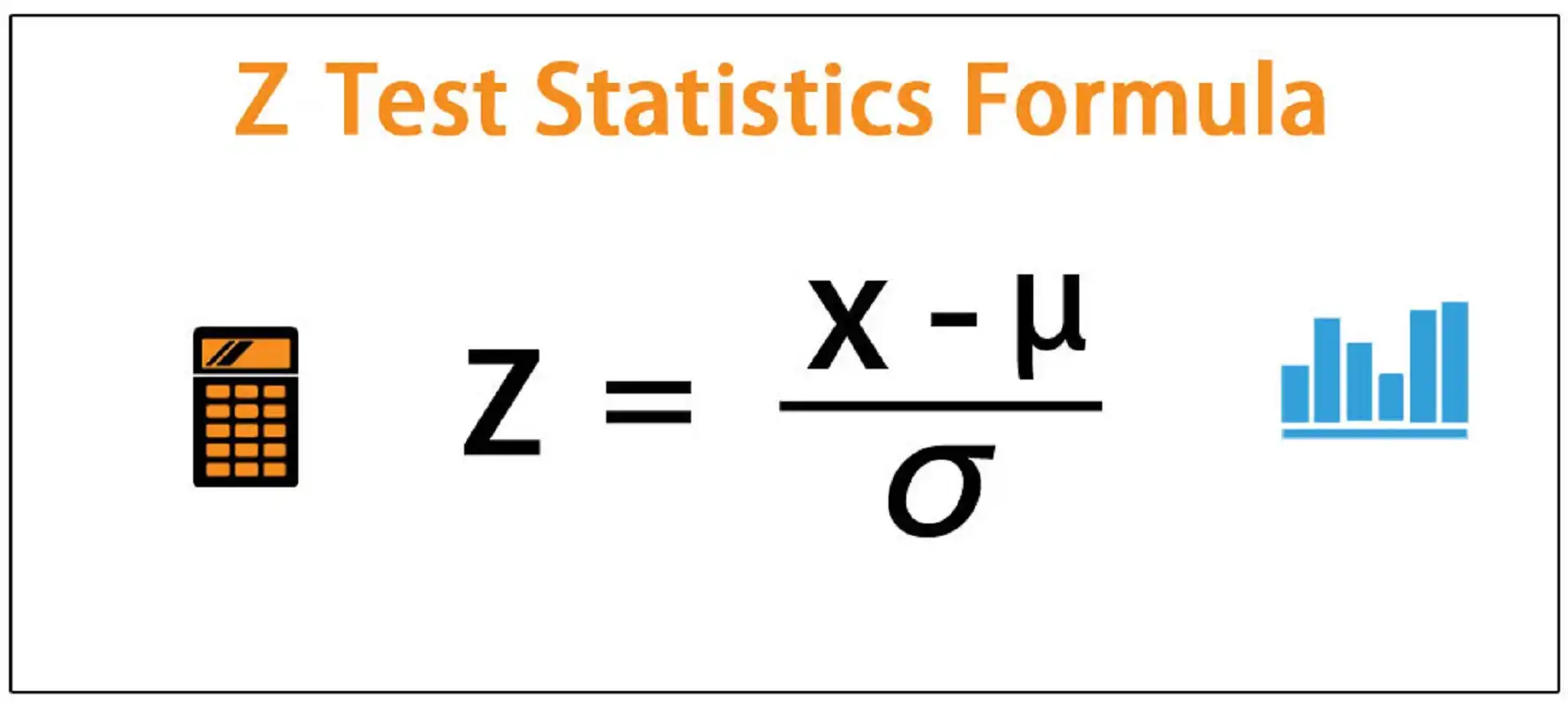
O teste Z, também conhecido como teste Z em estatística, é uma técnica amplamente utilizada para analisar dados e tomar decisões baseadas em evidências estatísticas. Neste glossário, vamos explorar em detalhes o que é o teste Z, como ele funciona e como pode ser aplicado em diferentes contextos.
O que é o teste Z?
O teste Z é um tipo de teste estatístico que compara uma média amostral com uma média populacional conhecida ou estimada. Ele é usado para determinar se há diferenças significativas entre a média amostral e a média populacional, o que pode indicar se uma determinada variável tem um efeito real ou se a diferença observada é devida ao acaso.
Para realizar o teste Z, é necessário ter uma amostra representativa da população em estudo e conhecer a média e o desvio padrão da população. Com base nesses dados, é possível calcular o valor do teste Z e compará-lo com um valor crítico para determinar se a diferença observada é estatisticamente significativa.
Como funciona o teste Z?
O teste Z é baseado na distribuição normal padrão, também conhecida como distribuição Z. Essa distribuição é simétrica e tem uma média de zero e um desvio padrão de um. A partir dessa distribuição, é possível calcular a probabilidade de obter uma determinada diferença entre a média amostral e a média populacional, assumindo que a hipótese nula seja verdadeira.
A hipótese nula no teste Z afirma que não há diferença significativa entre a média amostral e a média populacional. A hipótese alternativa, por sua vez, afirma que há diferença significativa entre as médias. O objetivo do teste Z é determinar se há evidências estatísticas suficientes para rejeitar a hipótese nula em favor da hipótese alternativa.
Para realizar o teste Z, é necessário calcular o valor do teste Z, que é dado pela fórmula:
Z = (X – μ) / (σ / √n)
Onde:
- Z é o valor do teste Z
- X é a média amostral
- μ é a média populacional
- σ é o desvio padrão populacional
- n é o tamanho da amostra
O valor do teste Z é então comparado com um valor crítico, que é determinado com base no nível de significância desejado. Se o valor do teste Z for maior do que o valor crítico, a hipótese nula é rejeitada e conclui-se que há diferença significativa entre as médias. Caso contrário, não há evidências suficientes para rejeitar a hipótese nula.
Aplicações do teste Z
O teste Z pode ser aplicado em uma variedade de situações e contextos. Algumas das aplicações mais comuns incluem:
Teste de hipóteses
O teste Z é frequentemente usado para testar hipóteses estatísticas. Por exemplo, um pesquisador pode querer testar se a média de uma variável em uma amostra é significativamente diferente da média populacional. O teste Z permite que o pesquisador tome uma decisão estatisticamente fundamentada com base nos dados coletados.
Comparação de médias
O teste Z também pode ser usado para comparar médias de duas amostras independentes. Por exemplo, um pesquisador pode querer saber se a média de uma variável é significativamente diferente entre dois grupos, como homens e mulheres. O teste Z permite que o pesquisador determine se há diferenças estatisticamente significativas entre as médias dos grupos.
Estudos de controle de qualidade
O teste Z é amplamente utilizado em estudos de controle de qualidade para verificar se um processo está funcionando corretamente. Por exemplo, uma fábrica pode querer testar se a média de um determinado parâmetro de qualidade, como a resistência de um produto, está dentro dos limites especificados. O teste Z permite que a fábrica tome decisões com base em evidências estatísticas.
Intervalo de confiança
O teste Z também pode ser usado para calcular intervalos de confiança para uma média populacional. Um intervalo de confiança é uma faixa de valores dentro da qual a média populacional é provável que esteja. O teste Z permite que o pesquisador determine a margem de erro associada ao intervalo de confiança.
Considerações finais
O teste Z é uma ferramenta poderosa para analisar dados e tomar decisões baseadas em evidências estatísticas. Ele permite que os pesquisadores testem hipóteses, comparem médias, realizem estudos de controle de qualidade e calculem intervalos de confiança. Ao entender como o teste Z funciona e como aplicá-lo corretamente, é possível obter insights valiosos a partir dos dados coletados.
